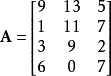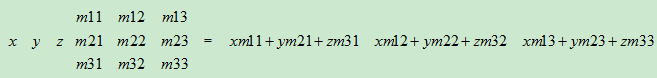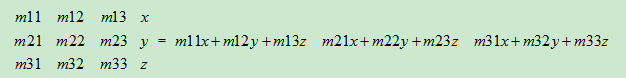矩阵是3D数学的重要基础,它主要用来描述两个坐标系系统间的关系,通过定义一种运算而将坐标系中的向量转换到另一个坐标系。
一、矩阵(数学)
- 数学定义:矩阵是以行和列形式组织的矩形数字块。前面说到过向量是一维数组,那么矩阵就是二维数组,向量是标量的数组,矩阵则是向量的数组。
- 矩阵的维度和记法:向量的维度定义为它所包含的数的个数,矩阵的维度被定义为它包含了多少行,多少列。一个 r × c 矩阵有 r行,c列。下面是一个4 × 3矩阵例子:
3. 方阵:行数和列数相同的矩阵称为方阵。 2 × 2 、 3 × 3 、 4× 4 方阵。方阵的对角线元素就是方阵中行号和列号相同的元素,其他元素均为非对角线元素。如果所有非对角线元素都是0,那么称这种矩阵为对角矩阵。对角线元素为1,其他元素为0的 n × n 矩阵称作为单位矩阵
4.矩阵乘法:某些情况下,两个矩阵可以相乘。(一个r × n矩阵A 能够乘以一个 n × c矩阵B,结果是一个 r × c矩阵 ,记作AB)例如:设A 为4×2矩阵,B为2×5矩阵,那么结果AB为4×5矩阵。如果A的列数和B的行数不匹配,则乘法没意义。
这看起来很复杂,其实这是一个简单的法则。对结果中的任意元素Cij ,取A的第i行和B的第j行,将行和列中的对应元素相乘,然后结果相加。Cij就等于这个和。
c24 = a21 · b14 + a22 · b24
5.向量与矩阵的乘法:因为向量能被当作是一行或一列的矩阵,所以能够用矩阵乘法与矩阵相乘。在这里,行向量和列向量相当重要。行向量和列向量乘以相同的矩阵得到的结果是不一样的。
如你所见,行向量左乘矩阵时,结果是行向量;列向量右乘矩阵时,结果是列向量。另外两种组合是不允许的。不能用行向量右乘矩阵,列向量左乘矩阵。
二、矩阵(几何)
- 向量从几何上能解释成一系列与轴平行的位移。
- 如果把矩阵的行解释为坐标系的基向量,那么乘以该矩阵就相当于执行了一次坐标系转换。
- 矩阵的每一行都能解释为转换后的基向量。